The goal of this section is to identify the Volume of Interest (VoI) on which to perform the quantitative analysis of epicardial fat. In particular, the first stage is to identify the anatomical structures in the CT scan corresponding to lungs, liver, diaphragm, sternum and ribs, in order to remove them from the VoI, since they do not contribute to epicardial fat. In addition, since the basal part of the heart (i.e. the volume containing the atria and the great vessels) is known to be more complex, its inclusion for the analysis of epicardial fat would require either strong manual intervention (leading to scarcely reproducible results) or extremely refined and knowledge-based segmentation methods. Thus, for the scopes of the present work, we focus on the analysis of the epicardial fat localized below the atrioventricular sulcus, i.e. in the regions corresponding to left and right ventricle. Indeed, the atrioventricular sulcus is an easily discernible pseudo-planar anatomical feature that can be certainly identified by experts, with very low inter-observer variability.

It is thus assumed that i) the acquired CT scan has been preprocessed by an expert, ii) the atrioventricular sulcus has been identified and iii) the volumetric dataset has been resampled along planes parallel to the sulcus. Formally, denoting with I = I (x, y, z) the volumetric dataset (where (x, y, z) ranges through the domain, namely a rectangular box 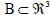), it is assumed the the planes with equation z = const are parallel to the intraventricular sulcus.

Under this assumption, some assisted image editing is still necessary for the identification of the VoI. Indeed the region corresponding to the heart should be separated from the nearby tissues. Since in computed tomography, the attenuation coefficient of lung tissue is well separated from the one corresponding to muscles and fat, lungs do not pose any problem, since they can be disregarded by simple thresholding. On the other hand, the intensity values of liver and diaphragm are similar to values found in the VoI. Thus, they cannot be separated merely on the basis of the intensity value. Another similar problem consists in the separation of fat depots near the chest wall from the epicardial fat. Also in this case, the separation cannot be based just on the local image appearance, but some complex vision system is required.

For the scopes of the present work, a simple form of manual intervention is introduced for these separation problems. Namely, an expert observer is required to scroll the slices between the atrioventricular sulcus and the apex and to place some control points on the pericardium. Such control points are automatically used to draw a natural cubic spline, which represents the closed pericardium contour, on each slice. A rasterization procedure is finally applied to convert the stack of splines into the volume V ⊂ B they bound. The volume V represents the identified VoI.

After having defined the VoI, a first rough estimation of epicardial fat is obtained by applying a threshold-based approach.

As reported in Section 1, absolute Hounsfield Unit (HU) values of voxels correspond directly to tissue property and, thus, epicardial fat may be identified by thresholding the VoI with the interval corresponding to adipose tissue (i.e. -190<HU<- 30 ). However, such nominal interval should be corrected on the basis both of the actual CT scanner and of the acquisition protocol (especially in case of contrast-enhanced images). In addition, it has been reported that the attenuation range varies also across population [15]. Thus, a tool has been designed for guiding the selection of a suitable interval [T₀ , T₁] to achieve the segmentation of epicardial fat, expressed as the following binary image J :

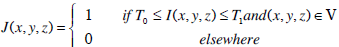(1)

In particular, if the segmentation obtained by the default interval ([T₀ , T₁] =[-190, - 30], using values in HU) is not satisfying, the cardiologist may proceed to the fine tuning of the the interval, for example by “probing” a patch of the image corresponding to epicardial fat. Indeed, the analysis of the histogram of the patch may be used to define a custom interval [T₀ , T₁]. More precisely, the following procedure is used:

1. Select a voxel P = (x_o , y_o , z_o ) in the interior of the region corresponding to epicardial fat.
2. Consider a cube C_o centered in P with edge length ℓ.
3. Compute the mean µ and the standard deviation σ of the volumetric dataset I restricted to the cube C_o.
4. Define the thresholds in the interval [T_o, T₁] by:
   
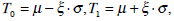
   where ξ is a positive real number. Notice that the interval is chosen with center µ and width proportional to σ.

The thresholding operated by Equation 1 provides a segmentation of epicardial fat which may suffer from spurious oscillations in the contour. A level set method is used to achieve both contour regularization and better adherence to image edges. Among several frameworks for level sets, we work slice-by-slice in the geodesic active contour framework [21], exploiting a variational formulation without contour re-initialization. Since the ultimate goal is to classify voxels inside the VoI with the labels fat and non-fat on the basis of their intensity, regional information is crucial and, thus, a region homogeneity term has been incorporated in the framework. More formally, consider for each slice z = z_k = cost , the region of interest R = V ᑎ {z = z_k} and let I_k(x, y) = I_k(x, y, z_k) be the induced two-dimensional image. Let {R⁺,R^-} be a partition of R into two disjoint regions corresponding to non-fat and fat respectively. Notice that the slice index k has been omitted to avoid cumbersome notation. Let be C the contour separating one region from the other. We look for an optimal C by minimizing a suitable energy functional E.

In the level set formulation, the contour C is represented as the zero-level set of a scalar function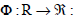

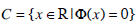(2)

In addition, the region R⁺ and (resp. R^-) is precisely the set on which Ф assumes positive (resp. negative) values.

Artificial time 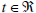is then introduced to evolve the contour towards a minimum value of the energy E. Taking as initial guess the partition 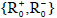given by the thresholding in Equation 1, we set:

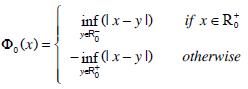(3)

Thus, the initial value Ф₀ at time t = 0 is set equal to the Signed Distance Function (SDF) from the contour. Of course several other choices for the function Ф₀ may be used to encode the same initial contour, however -as it is well known- initializing the level set function with a SDF is suitable for achieving stability in numerical approximations.

For example, a SDF is almost everywhere differentiable (actually 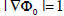as we will see in Section 2.3.3), reducing numerical inaccuracy that may show up during contour evolution.

A composite energy term was associated with Ф_t, expressing the goodness of contour fitting to the image data and inner conditions of homogeneity and stability:

(4)

Each of the summands in Equation 4 achieves a special effect and, for sake of clarity, they will be discussed separately in the sections below.

2.3.1. The Geodesic Active Contour Term

As usual, let the edge indicator functiong be defined as:

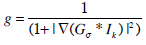(5)

where G_σ is a Gaussian kernel with variance σ².

The first summand E_GAC in Equation 4 is defined as:

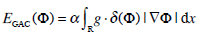(6)

where the integral is extended to the whole region R, α is a positive constant and δ is the Dirac delta function. The term E_GAC corresponds to the length of the contour C weighted by the edge indicator function. Requiring that the length of the contour is minimal is a well-known condition for achieving smoothness, since spurious contour oscillations are wiped out. Minimizing g -weighted length achieves instead simultaneously contour smoothness and adherence to image data. In particular, notice that a piece of contour crossing an homogeneous region is discouraged, since the region is characterized by high values of g (namely g ≈ 1). By contrast a piece of contour on an ideal edge costs nothing, since g = 0 there.

2.3.2. The Region Homogeneity Term

The E_RH term is specially designed for favoring the selection of homogeneous regions. Namely, we suppose that the intensities of voxels belonging to R⁺ and R^- are drawn from two distinct probability density functions, being p⁺ and p^- respectively.

After a careful analysis of the histograms of the region of interest, it has been judged convenient to model both distributions by using Gaussian Mixture Models (GMM), with N⁺ and N^- components respectively:

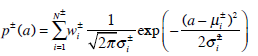(7)

where 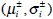are the mean and standard deviation of the i-th Gaussian distribution and 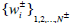are the weights of the mixture.

Assuming that voxels are independent and identically distributed, the conditional probability of the image I_k given a partition {R⁺, R^-} is given by:

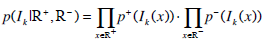(8)

Applying the logarithm to Equation 8, we have:

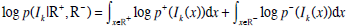(9)

This in turn suggests to define the following energetic term for region homogeneity (see also [22]):

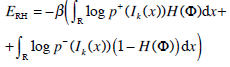(10)

where β is a positive constant and H denotes the Heaviside function, defined as:

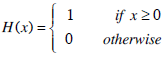(11)

2.3.3. The SDF Constrain Term

For the introduction of the last, technical summand E_SDF, recall that we chose Ф₀ to be a SDF, for several numerical advantages. In usual level set formulation, Ф_t ceases to be a SDF as the time evolves. This can lead to less confident estimations of the derivatives in usual finite difference schemes and, eventually, the functions Ф_t may develop shocks. To avoid this, it is customary to periodically re-initialize Ф_t to a SDF. Several strategies exist for achieving this goal, for example by applying some iso-contour algorithm and, then, computing the SDF again or by solving the so-called re-initialization equation, i.e. another partial differential equation. However, none of this method is appealing, because it is difficult to decide when and how often to perform re-initialization. The strategy we adopted consists in softly constraining Ф_t to be a SDF during the whole evolution [23].

To discuss this issue, we first recall that a SDF Ψ satisfies:

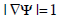(12)

in every point having one and only one closest point and, thus, generically. It is not difficult to show that the converse also holds, i.e. any function Ψ satisfying 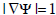is a SDF. This differential characterization of signed distance functions is suitable for the present purpose. Actually defining

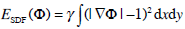(13)

we have a measure of how close Ф is to a signed distance function. A positive constant γ is introduced to manage the tradeoff with the previous energy terms. During contour evolution, the E_SDF the term prevents Ф_t to move away from the space of signed distance functions. In this way, numerical inaccuracy are avoided, retaining the good features of a SDF, without any need of other numerical remedies.

2.3.4. Energy Minimization

The minimization of the functional E is performed by gradient descent, using the initialization described in Equation 3:

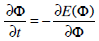(14)

where 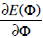is the first variation of the functional E By linearity:

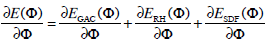(15)

It is not difficult to compute these first variations, which are given by:

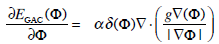(16)

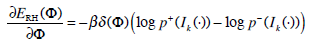(17)

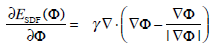(18)

In the numerical discretization, all these quantities are approximated by a first order standard finite difference scheme.

After having applied the previous method to each slice, the direct computation of global parameters for the evaluation of epicardial fat is straightforward. In particular, the area A_k of the region corresponding to epicardial fat may be computed in the slice z = z_k by the formula:

(19)

where Ф is the optimal function found minimizing the functional in Equation 4 and H is the Heaviside function defined in Equation 11. Notice that there is no need to define a crisp segmentation, i.e. for example by extracting a binary mask from Ф . Using a mollified Heaviside function, partial volume effects near the interface may be also controlled. Let ∆ be the interslice spacing in the dataset. The total epicardial fat volumeV_fat may be estimated by the sum:

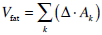(20)

where the summation runs over all the slices between the atrioventricular sulcus and the heart apex.

For clinical applications, it is convenient to normalize the total fat volume by the Body Surface Area (BSA), thus defining a fat index:

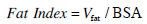(21)

Besides total volume, we started to analyze the regional distribution of epicardial fat depots. To this end, the volume of fat surrounding each ventricle is estimated. For this analysis, the user is asked to locate, in the original images, the plane separating the left from the right ventricle. Such a plane can be easily and reproducibly identified according to a well-defined anatomical landmark, i.e. the interventricular sulcus.

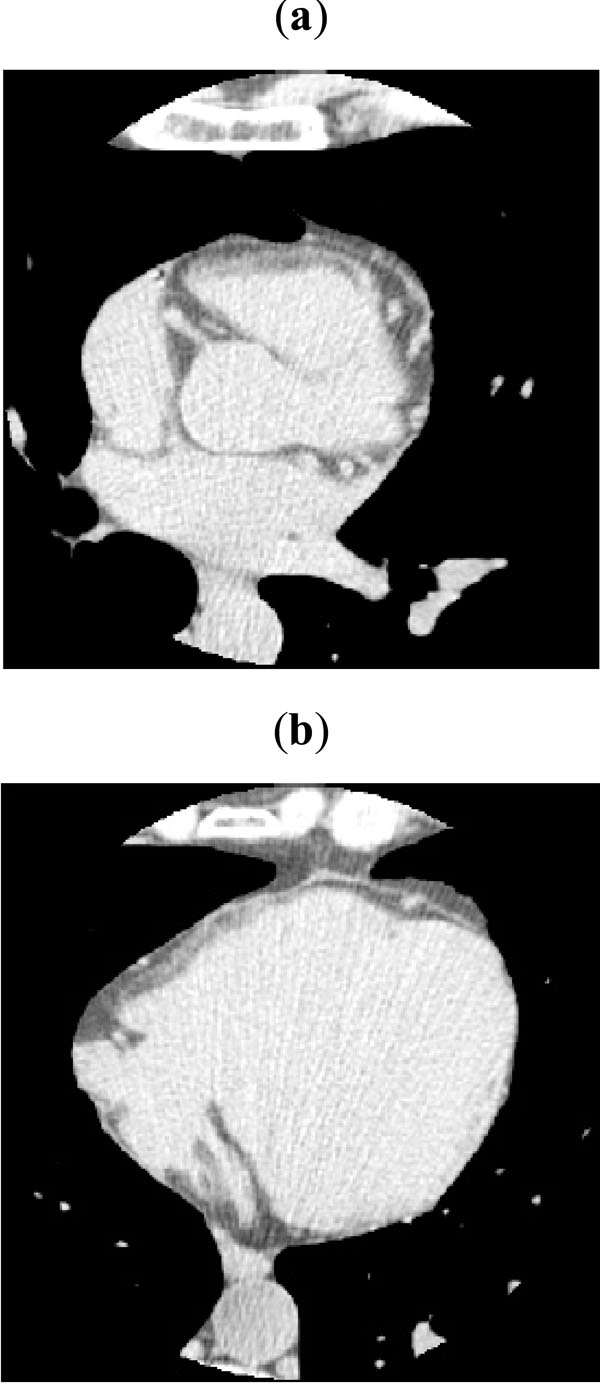
The procedure was tested on CT images obtained during standard calcium scoring CT studies. Cardiac CT examinations were performed using a GE Light- Speed 64 VCT scanner. Patients were pretreated with proponolol (2 mg i.v.) and isorbide denitrate (0.6 mg i.v.) as clinically indicated. After the scout of the thorax, the heart volume was scanned to obtain the images for calcium scoring. Slices with voxel size 0.625 × 0.625 × 2.5 mm were so obtained without contrast medium injection. Ten patients have been used for testing the procedures described in this paper. Examples of acquired images are given in Fig. (1).

Fig. (1). Typical slices acquired in the calcium scoring case. In the slice (a) some portion of atria and great vessels are visible, while slice (b) shows a separation problem between the heart and the chest wall. Hounsfield values between and are represented.

Fig. (2). Typical views of the dataset obtained after resampling in planes parallel to the atrioventricular sulcus: (a) saggital view and (b) axial view. Notice that in (a) the atrioventricular sulcus is easily discernible.

Fig. (3). Axial views of the identified VoI: (a) apical, (b) mid and (c) basal slice planes. The green curve is the natural cubic spline whose control points have been placed by an experienced observer.

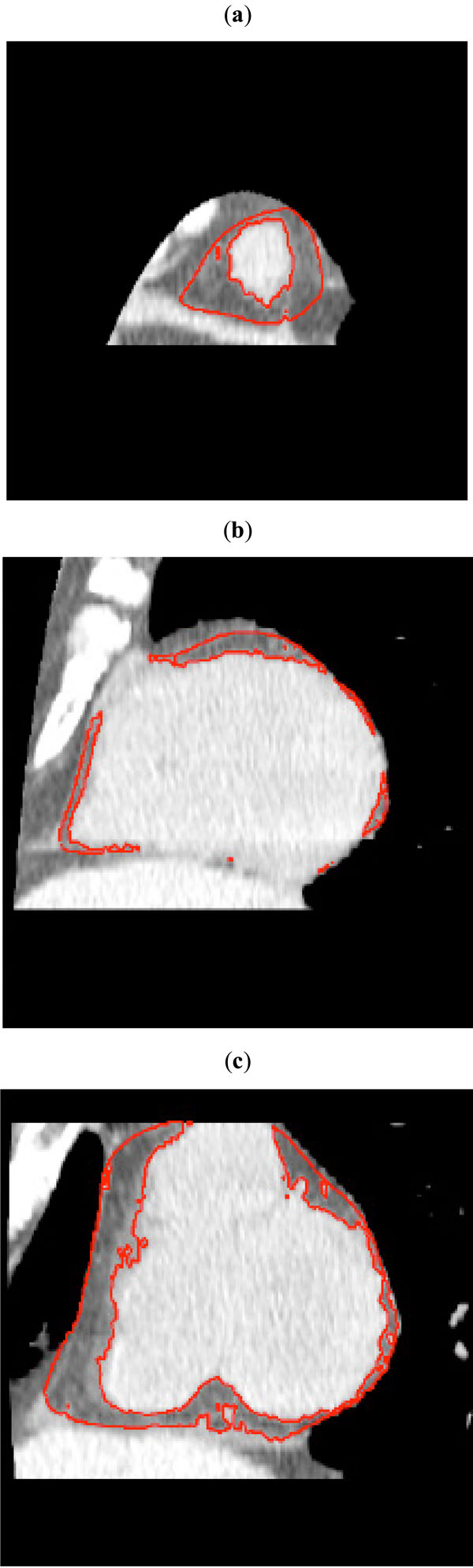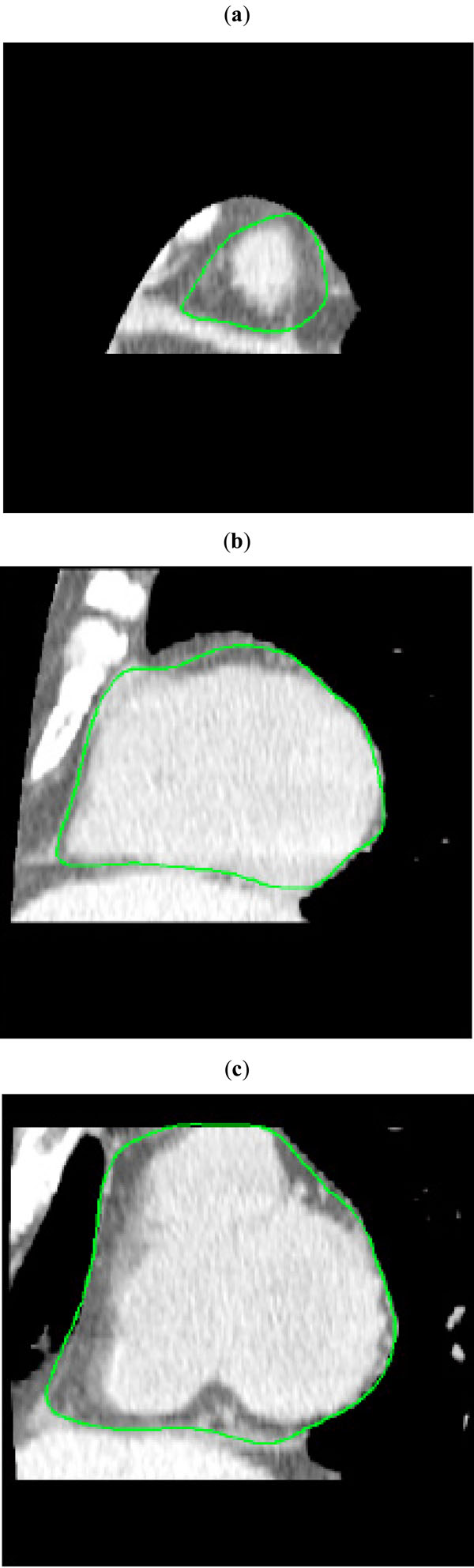
Fig. (4). First segmentation of the epicardial fat by thresholding: (a) apical, (b) mid and (c) basal slice planes. The red curves encircle epicardial fat depots.

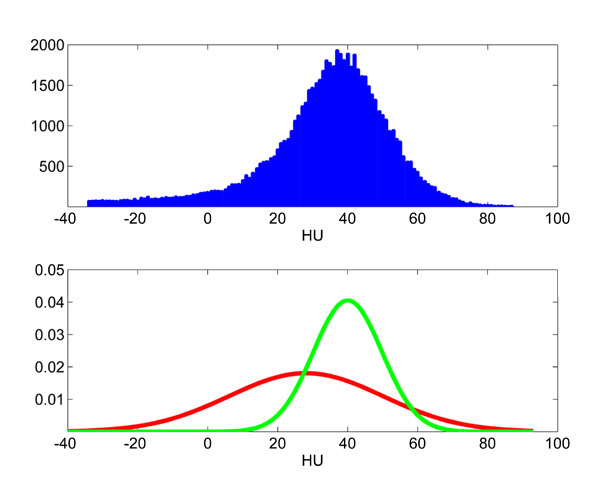Fig. (5). Intensity distribution of the non-fat region from Fig. (4b) and plot of the two Gaussian distributions from the estimated GMM.

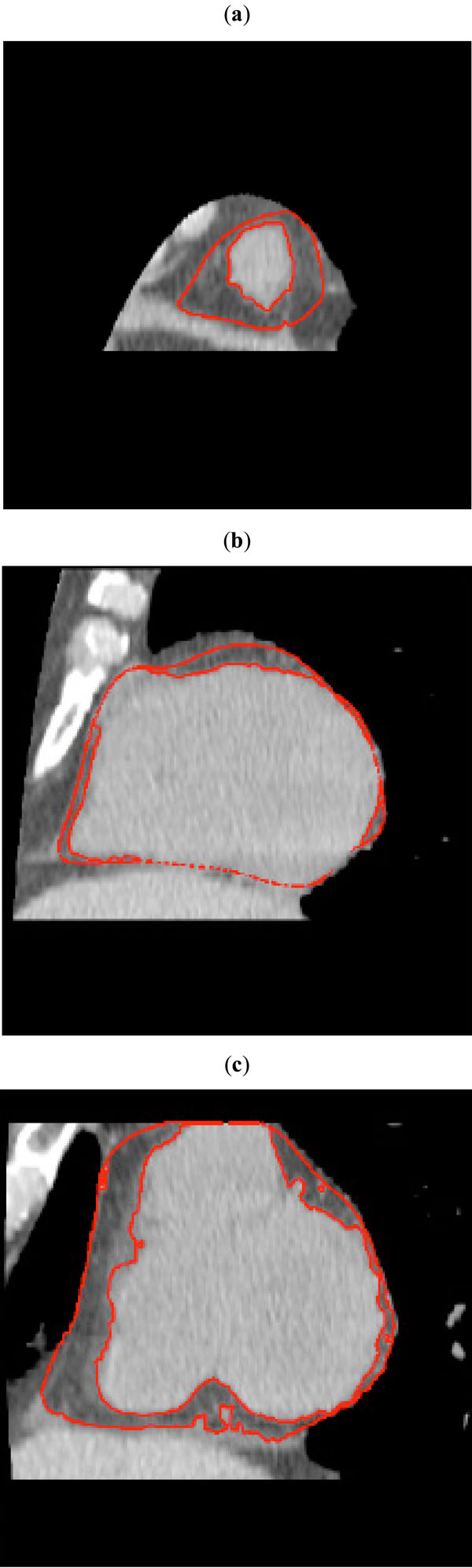Fig. (6). Level set refinement of the epicardial fat segmentation: (a) apical, (b) mid and (c) basal slice planes. The red curves encircle fat depots. Improvement of smoothness with respect Fig. (4) may be appreciated.

Fig. (7). Views of the global segmented volume: (a) axial, (b) coronal and (c) sagittal views. Epicardial fat is shaded in blue, while internal heart is shaded in pink.

Fig. (8). 3D reconstruction of the segmented volume.

After the expert has identified the plane H on which the atrioventricular sulcus approximately lies (see Section 2.1), the original images acquired by the CT scanner were resampled along planes parallel to H. The volume was discretized by a grid of size (n_x , n_y , n_z ) = (512, 512, 62) . Since the spatial resolution of the datasets is high, no significant artefact was introduced by resampling. Examples of the resampled volumetric dataset are shown in Fig. (2).

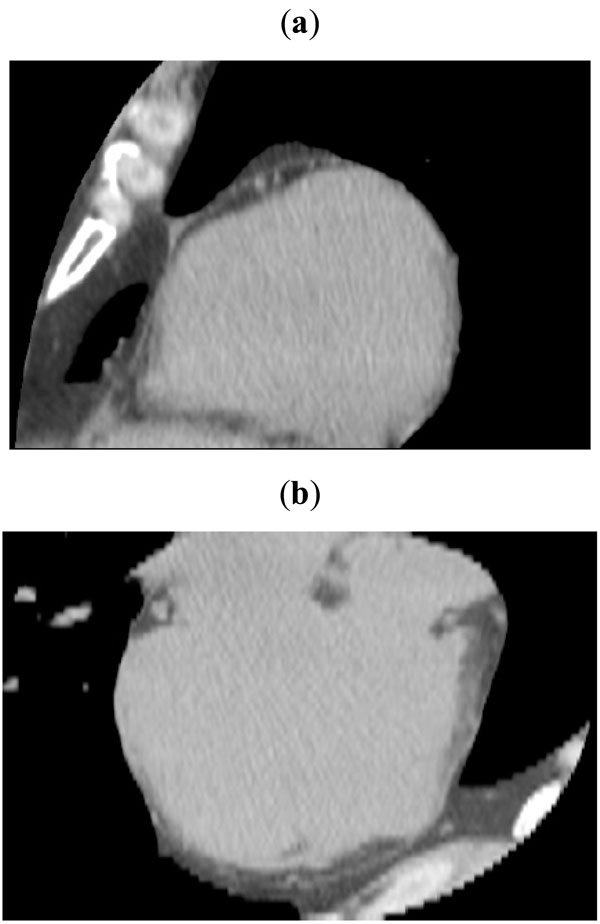
The volume was then edited as described in Section 2.1, obtaining as a result a VoI containing all the voxels that may contribute to epicardial fat volume. Some views of the VoI are shown in Fig. (3), together with the natural cubic spline curve delineated by an experienced observer.

The plane separating the left and right ventricle, identified through the interventricular sulcus, is also traced with some standard user interaction.

After identification of the VoI, the threshold-based segmentation was performed. For the choice of the interval [T₀ ,T₁ ], a voxel in the interior of the epicardial fat region was selected. A cube C₀ having edge length ℓ = 6,25 mm was considered, obtaining as values µ = - 115 HU and σ ≈ 35 HU. The parameter ξ was manually set to 2. As expected, it resulted that µ is robust with respect to the choice of the voxel and of the length ℓ. Fig. (4) shows the segmentation obtained from the slices in Fig. (3) by thresholding according to the determined interval [T₀ ,T₁]=[-185, -45] HU.

The level set refinement method was then applied slice-by-slice. Using the initial guess provided by thresholding, GMMs with N⁺ = N^- = 2 modes were fitted to the data, using the Expectation-Maximization algorithm [24]. An example is shown in Fig. (5).

Visual evaluation of the segmentation results lead to the choice of the parameters α,β,γ involved in the summands in Equation 4. In particular, the following values were used throughout the study:

α=2    β=10^-3    γ=0.2

A time-step ∆t = 3 was deemed suitable and 30 iterations in the gradient descent brought to the results reported in Fig. (6). After applying such refinement to all the slices, the final segmentation of the epicardial fat could be inspected by using the conventional views reported in Fig. (7), where tissues of interest have been shaded. The geometry of epicardial fat was also reconstructed applying the marching cube isosurfacing algorithm. An example is shown in Fig. (8). For this particular patient, a V_fat =78 cm³ was computed, which leads to a Fat Index =41 cm ³ / m ².