RESEARCH ARTICLE
Medical Image Encryption: An Application for Improved Padding Based GGH Encryption Algorithm
Massoud Sokouti1, Ali Zakerolhosseini2, Babak Sokouti3, *
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 11
Last Page: 22
Publisher Id: TOMINFOJ-10-11
DOI: 10.2174/1874431101610010011
Article History:
Received Date: 2/4/2016Revision Received Date: 11/8/2016
Acceptance Date: 12/8/2016
Electronic publication date: 28/10/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
Medical images are regarded as important and sensitive data in the medical informatics systems. For transferring medical images over an insecure network, developing a secure encryption algorithm is necessary. Among the three main properties of security services (i.e., confidentiality, integrity, and availability), the confidentiality is the most essential feature for exchanging medical images among physicians. The Goldreich Goldwasser Halevi (GGH) algorithm can be a good choice for encrypting medical images as both the algorithm and sensitive data are represented by numeric matrices. Additionally, the GGH algorithm does not increase the size of the image and hence, its complexity will remain as simple as O(n2). However, one of the disadvantages of using the GGH algorithm is the Chosen Cipher Text attack. In our strategy, this shortcoming of GGH algorithm has been taken in to consideration and has been improved by applying the padding (i.e., snail tour XORing), before the GGH encryption process. For evaluating their performances, three measurement criteria are considered including (i) Number of Pixels Change Rate (NPCR), (ii) Unified Average Changing Intensity (UACI), and (iii) Avalanche effect. The results on three different sizes of images showed that padding GGH approach has improved UACI, NPCR, and Avalanche by almost 100%, 35%, and 45%, respectively, in comparison to the standard GGH algorithm. Also, the outcomes will make the padding GGH resist against the cipher text, the chosen cipher text, and the statistical attacks. Furthermore, increasing the avalanche effect of more than 50% is a promising achievement in comparison to the increased complexities of the proposed method in terms of encryption and decryption processes.
1. INTRODUCTION
Image encryption is one of the important fields of cryptography and one of the best known algorithms used in this realm is the DES (Data Encryption Standard) algorithm which requires less time while considering the computational costs [1, 2]. A digital image can be considered as a two dimensional matrix or a square array of numbers. The elements of this array are called pixels. The value of these pixels are digital numbers and since we can show it as a matrix that each pixel can be denoted by a position as (row, column). By encrypting an image, it is meant to apply a symmetric or asymmetric encryption algorithm on an input image to be converted into a cipher image using either symmetric or asymmetric keys [3, 4]. Symmetric ciphers only use one key for encryption and decryption processes while asymmetric ciphers use two different key pairs (i.e., public and private keys) [5].
An encryption/decryption algorithm is considered as strong while it can resist against most well known attacks such as known-plaintext and ciphertext-only attacks [6]. One of the most important topics in exchanging sensitive information among medical physicians is to provide security for medical images. Thus encryption methods are necessary to provide a robust secure environment for both data and images. The sameness property in recent algorithms make them easy to be broken, so for this purpose a simple lattice based public key encryption algorithm can be implemented by using the Goldreich Goldwasser Halevi (GGH) based on numeric matrices. The important factors which makes the GGH algorithm fitted best for medical image encryption are: (i) it is based on public key cryptosystem, (ii) it has a numerical matrix/lattice based scheme which is suitable for images, and (iii) it has the low calculation cost and fastness properties. Based on the architecture of the GGH encryption algorithm, the size of ciphered image will be the same as the original image, but the bit sizes of cipher image will be increased while being compared to the original image. The other advantage of the GGH for image encryption is placed in the decryption process. Most of the time, GGH produce errors in decrypted data and makes it inaccurate as this error exists only at the right LSB bits (least significant bits), so the pixel will not change a lot and hence, the original image can be retrieved easily. The other best known lattice based cryptography is NTRU. NTRU can work as well as GGH but it can have some problems in encryption. NTRU uses negabinary system, so this can increase the size of the matrix by four times and it can reduce the computation speed in high resolution images. On the other hand, if an error occurred in the decryption process, this error may be at the MSB (Most significant bits) bits and can destroy the pixels of the image. That is why NTRU is not suitable for image encryption frameworks. The paper is organized as follows: starting with the literature reviews, the GGH algorithm, implementation of the proposed algorithm, and results and discussion followed by conclusions and future works.
Image transmission among clinicians through insecure Internet is one of the most important applications of medical image encryption. The effectiveness of the Cipher Feedback Mode (CFB) has been widely used in securing the images [7]. To achieve a high degree of encryption in this method, the input data sizes are 8 bits, 16 bits, and 32 bits and the feedback blocks are evaluated by using the entropy parameter and then measuring the gray level distribution. It means, for a 28=256 gray level image, the entropy increases when the distributed gray level pixels of the image increases. It is shown that while the input data and feedback blocks have the same size, CFB encryption mode approximately results in an optimized entropy [8].
A secret sharing scheme (k, n) based on polynomial interpolation was presented by Shamir [9]. Based on Shamir’s secret sharing scheme, the medical images will be shared among clinicians that prevent eavesdroppers from accessing the medical images transmitted between two clinicians. If any k of n is presented, the medical images and their corresponding patient information can be recovered using the retrieving procedure. The details of this process are summarized in two procedures including the partitioning and retrieving. In the partitioning procedure, the unique x values are determined for each participant. Then, the sharing algorithm which is used for inter-communicating between dealer and participants, medical images, and patient information are divided into shares [10]. The results are noisy images, which attract the attacker's attention. Finally, by applying the optimal pixel adjustment process, the attraction can be reduced and for each participant, a certificate will be issued for its protection. In the retrieving procedure, image integrity authentication is the goal of this phase. Then, the medical image should be recovered. After that, a row-column transposition procedure is applied to the block pixels. Shamir proposed a secret sharing scheme based on polynomial interpolation [9]. Their proposed method shared medical images between n clinicians in which at least k of them are present. In 2008, Hill cipher algorithm has been implemented as one of the encryption methods for images at both gray and color scales [11]. However, this method failed on the background of images which were at the same level of color attributes. Nag and his colleagues took the advantages of positions of pixels within the target images [12]. In the next step, the affine transform was applied to change the pixel positions using four keys. Finally, the divided blocks will be XORed in order to encrypt the images. Their results showed that the correlation between the plain image and the encrypted image was so small. Sokouti et al. [13, 14], proposed a genetic-based random key in an one time pad (OTP) encryption system using the image bits. The image was split into row blocks for encryption purpose. After the encryption process, because of its double-numerical nature, no one will recognize whether it is an encrypted image or a text. Regardless of its random keys, OTP encryption system, and numerical nature, it will be turned to be a high secure medical image encryption system in which the security management policies should be complied with the recent security standards to keep it safe forever. In another study, other authors presented a modified version of AES encryption algorithm by incorporating a key stream generator [7]. Although, it has a good performance, however, it lacks a good computational cost. Moreover, another encryption algorithm was presented and the resulted image was significantly decreased the correlation among the elements with high entropy [11]. The method was implemented based on Hill cipher and since it uses matrices for encryption, so it is a suitable algorithm to be used for image encryption. In another research [15], a new method by including both permutation and encryption methodologies was proposed. The idea of this algorithm is to divide an image into 4 pixels block, the permutation and encryption by RijnDael algorithm process will be performed, respectively. Based on the reported results, the similarity between the original and encrypted images was decreased with an increasing trend on the entropy values. In Seyedzade et al. [16], the SHA-512 hash function based on XOR operation was used for image encryption. The method has very few chances of errors and also, it is a very slow algorithm. In Ismail IA et al. [17], an algorithm for image encryption was deployed by using two chaotic logistic maps with a large 104-bit key space. These are used to make more different pixels while the cipher and the plain images are being compared. Actually, the plain pixel depends on key and the output depends on the logistic map and hence, the confusion will be increased. In Kamali SH et al. [18], the modified version of AES (MAES) was presented in which the security properties were highly increased in comparison to AES. In Indrakanti et al. [19], the method is based on random pixel permutation to maintain the quality of the image with less computation, fast encryption, and high error chance. There are three phases in this method including the image encryption, key generation, and identification process. In Enayatifkr et al. [20], a hybrid algorithm which took the advantages of both genetic algorithm and chaotic function was presented. At the fist stage, the first population was generated. This population includes the initial image on which the chaotic function is applied. Finally, in this method, the best encryption result will be chosen. In Singh K et al. [21], a cross chaotic maps with the incorporation of DNA was presented which had better results than a default based chaotic maps and counted as an easy and cost effective method. In Alsafasfeh QH et al. [22], the authors added Lorenz and Rossler chaotic systems in to their proposed word which had better and robust characteristics in terms of speed, key space, and security. In Abuhaiba et al. [23], they encrypted an image using differential evolution. Several analyses were conducted on security properties such as key space analysis and statistical analysis, to mention a few [24]. In Abugharsa AB et al. [25], a new AES based technique was incorporated on shifting blocks of divided images, and applying rows and columns shuffling, and then encrypting by AES algorithm with some errors in a long process. In Pareek NK et al. [26], a non-chaos based image encryption method using external 144-bits key was presented. It incorporates the pixel permutation substitution, so, it is strong against the differential attack with a high encryption rate, less computational cost, and less changes in keys. In Agarwal A et al. [27], a genetic algorithm based methodology was presented which had really a long process while considering its computational costs and the flowchart. In Bhatt V et al. [28], a method comprising of the position permutation, value transformation, substitution, and transposition was represented with very slow process and high entropy.
2. MATERIALS AND METHODS
2.1. Lattice
Any lattice is a set of points in an n-dimensional space which has a periodic structure [29-31]. Let
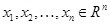 as n-linear independent vectors, the lattice generated by them is a vector defined as equation (1):
as n-linear independent vectors, the lattice generated by them is a vector defined as equation (1):
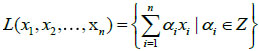 |
(1) |
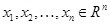 vectors are the basis of the lattice.
vectors are the basis of the lattice.
The first lattice-based cryptography based on worst-case problem was presented by Ajatai and Dwork in1997 [32]. After that, there have been a lot of improvements over lattice-based cryptography algorithms. In 1997, Goldreich, Goldwasser, and Halevi also presented a lattice-based cryptography based on closest vector problem (CVP) [33]. In 1998, Hoffstein and Silverman, presented a new lattice-based cryptography using the shortest vector problem (SVP) which works on polynomials [34].
2.2. GGH Algorithm
In this study, we have taken the advantage of the GGH algorithm for encrypting the clinical images. The GGH cryptosystem is based on CVP which is one of the NP-hard problems presented in 1997 by Goldreich et al. [33]. It also introduces a trapdoor as an one-way function for implementing a public key cipher which relies on difficulty of lattice reduction. However, this algorithm was first cryptanalyzed by Phong Q. Nguyen in 1999 [35]. This system was a suggestive framework of the McEliece cryptosystem [36]. For both systems, encryption is randomly performed. The basic GGH public key encryption system is similar to McEliece cryptosystem. The two parameters on which GGH relies, are lattice dimension (n>200) and the security parameter (σ). The security parameter presents the difficulty of the CVP. The authors of GGH, published some challenges for the security parameters as n=200, 250, 300, 350 and 400. Nguyen attacked all of the challenges except for n=400, since the key size was too large [35]. The private key is a secret matrix R and its columns are comprised of a basis of a Lattice
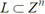 . The parameters of GGH are shown in Table 1 where the basis consists of the short integral vectors. There are several methods to construct the secret basis r. Two methods to generate the nice basis R are to choose a random matrix r within entries, (i.e., all vectors are chosen relatively short) and to choose r= k.In+E where In is the n×n identity matrix, k>1is a medium sized integer, and E is a random matrix with small entries, as mentioned above. The public key is a public matrix denoted by B, which represents another basis for L. The public basis is known as a bad basis as it is not reducible as the secret basis. There are several methods which can randomly generate the public basis B from the secret basis r.
. The parameters of GGH are shown in Table 1 where the basis consists of the short integral vectors. There are several methods to construct the secret basis r. Two methods to generate the nice basis R are to choose a random matrix r within entries, (i.e., all vectors are chosen relatively short) and to choose r= k.In+E where In is the n×n identity matrix, k>1is a medium sized integer, and E is a random matrix with small entries, as mentioned above. The public key is a public matrix denoted by B, which represents another basis for L. The public basis is known as a bad basis as it is not reducible as the secret basis. There are several methods which can randomly generate the public basis B from the secret basis r.
| Parameter | Description | Knowledge |
|---|---|---|
|
n σ R B |
Dimension Security Parameter Integral matrix n×n Integral matrix n×n |
Public Public Private Public |
In 1999, Micciancio used Hermite Normal Form (HNF) for improving public key generation to reduce the size of the key [29, 37]. For generating the public key B from the private key R, a unimodular matrix U is required as shown in equation (2):
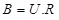 |
(2) |
Now, assuming the message matrix as m and error matrix as e, the cipher matrix c is calculated as below:
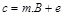 |
(3) |
To decrypt this cipher, the calculations are performed according to the following equations:
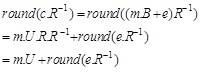 |
(4) |
The Babai rounding technique will be used to remove the term as it is a small value. Finally, the message matrix m will be calculated as follows:
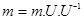 |
(5) |
If round (e.R-1)=b is a nonzero vector, the Rb will be a nonzero lattice vector. In this case, the Babai's rounding will not return the lattice point and hence, the wrong message will be retrieved. The decryption process will work correctly when round (e.R-1)=0. This will be possible when σ is small enough since the error vector is chosen from the vector (±σ, ±σ, ±σ, ..., ±σ) . The increment of σ will increase the distance between the lattice vector m and the cipher text c. By increasing the distance, the CVP will become harder. When round(R-1e)≠0 the probability of decryption error increases. The size of key and the complexity of this cipher are shown in Table 2.
| Object | Size(bits) | |
| GGH | Padding GGH | |
| Private key R Public key B |
n2log2(k) n2log2(n) |
n2log2(k) n2log2(n) |
| Operation | Complexity | |
| GGH | Padding GGH | |
| Key Generation | n3 | n3 |
| Encryption | n2 | 2n2 |
| Decryption | n2 | 2n2 |
3. THE PROPOSED PROTOCOL
Suppose Bob is the receiver and Alice is the sender. He chooses an image, reduces the pixel values mod 5 and takes this image as his private key. Then, he generates a unimodular matrix, randomly. He uses the equation (2) to calculate the public key. Then, Bob sends the public key image to Alice. Alice uses Bob’s public key image to encrypt the clinical image or plain image using the equation (3). The cipher is a noisy image which is sent to Bob. Bob receives the cipher image and uses his own private key image and the unimodular matrix to decrypt the received image into an original clinical image using equations (4) and (5).
3.1. Applying Two Snail Tour XORing to the Standard GGH Algorithm
In this section, we present a new method by applying padding before performing the GGH encryption. The padding process uses two snail tours XORing techniques; forward and backward, since we want to affect one pixel change in the entire matrix. The moving structure of applying forward and backward snail tours methodologies are shown in Fig. (1A and 1B), respectively. After applying the forward snail tour, we will XOR the pairs according to the equation (6):
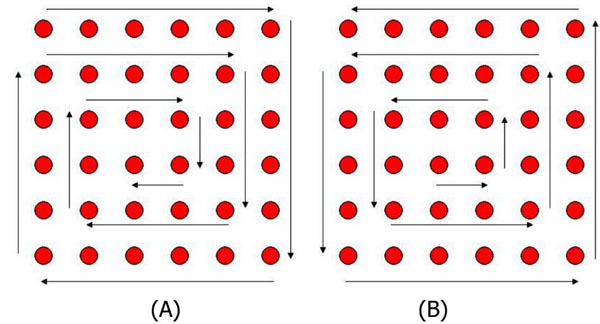 |
Fig. (1). (A) Forward Snail tour in matrix 6×6 (B) Backward Snail tour in matrix 6×6. |
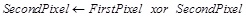 |
(6) |
After that, a backward snail tour will be applied and XORing of the pixel pairs will be done by using equation (6). After applying the padding, the new resulted matrix will be encrypted using GGH encryption algorithm. The decryption process is also based on the GGH decryption algorithm. Now, it is time to decrypt the padding of matrix. For removing the padding, a forward snail tour will be applied but this time by XORing pair of pixels according to the equation (7).
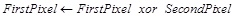 |
(7) |
The algorithms of encryption and decryption processes are shown below as Algorithms 1 and 2, respectively. Algorithms 1.GGH_Snail_Encryption
 |
Algorithms 2.GGH_Snail_Decryption
 |
4. RESULTS AND DISCUSSION
The GGH clinical cipher system has been implemented in Matlab 6.5 programming software. All the employed images are at the grey scale level. To encrypt a clinical image, at first, it has been resized into 200×200 pixels as illustrated in Fig. (2A). Another image will be chosen and reduced by mod 5 as the private key which will be read and resized to 200×200 pixels are shown in Fig. (2C). A random matrix with size 200×200 where det = 1,- 1 will be generated randomly as shown in Fig. (2D). Note that the size of 200×200 pixels is a sample size and any arbitrary size can be chosen for this step but it should be a square size and the larger the size, the more the lattice reduction will be difficult to be broken. According to the equation (2), the public key matrix is calculated as shown in Fig. (2B). In this step, the private key and the unimodular matrix images are used for decryption process. The next step is to encrypt the clinical image using the public key image. The cipher image which is produced according to the equation (3) is shown in Fig. (2E). After the image has been encrypted, the receiver receives the encrypted image, he will multiply the inverse of private key to cipher matrix according to the equation (4) and the result is shown in Fig. (3A) By calculating the inverse of unimodular matrix and calculating it according to the equation (5), the message will then be decrypted as shown in Fig. (3B).
 |
Fig. (2). (A) Clinical plain image 200×200 (B) PRIVATE key image 200×200 (C) Unimodular key image 200×200 (D) Public key image 200×200 (E) Encrypted(Cipher) image 200×200. |
 |
Fig. (3). (A) First step of decryption 200×200 (B) The decrypted message 200×200. |
Now, the new proposed algorithm will be applied to the plain clinical image which is shown in Fig. (2A). The result of applying two snail tour XORing to the plain clinical image is shown in Fig. (4A). After that, the GGH encryption algorithm will be applied to the new padding plain image (Fig. 4A) by using the public key image which is presented in Fig. (2B), and finally the encrypted result is shown in Fig. (4B).
The decryption process of the cipher text will be performed using the private key image (Fig. 2C) which should be then reduced by mod 5 and unimodular matrix image (Fig. 2D) and the decrypted image using the GGH algorithm is shown in Fig. (4C). Then, the applied padding will be reversed according to two snail tour XORing and the decrypted image is shown in Fig. (4D).
For evaluating the encryption level of this image, we will focus on the differential attack. In this attack, attacker tries to understand the relationships between the plain and the cipher images. The attacker studies the effect of changing in one pixel of the input on the whole pixels of output cipher image to determine the key. To measure the effect of each pixel on the whole encrypted image, we can use three common security evaluations metrics [38]:
1. Number of Pixels Change Rate (NPCR):
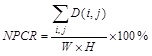 |
(8) |
Where D(i.j) is the value of pixel difference in plain and cipher images at position (i,j) and W is the width of the matrix and H is the height of the matrix.
2. Unified Average Changing Intensity (UACI):
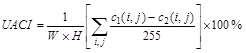 |
(9) |
Where C1, C2 are two ciphered images that their corresponding original images have only one pixel difference. Notice that C1, C2 are in the same size. C1(i, j), C2(i, j) are gray-scale values of the pixels at grid(i,j). D(i, j) is determined by C1(i, j) and C2(i, j) if C1(i, j)≠C2(i, j) then D(i, j)=1; otherwise, D(i, j)=0 (W and H are the columns and rows of the image).
3. Avalanche effect which shows the number of bits that are changed and is calculated according to equation (10).
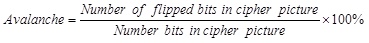 |
(10) |
To evaluate the new GGH snail tour encryption algorithm, three abovementioned evaluation metrics are considered on the images of three groups containing 100 images, Group 1 are images with size 50×50, group 2 are images with size 100×100, and group 3 are images with size 200×200. The comparison results between the padding based GGH and standard GGH algorithms are illustrated in Table 3.
| Method -> | Improvement | Padding based GGH | Standard GGH | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Size | NPCR% | UACI% | Avalanche% | NPCR% | UACI% | Avalanche% | NPCR% | UACI% | Avalanche% |
| 50×50 | 98 | 34.88 | 44.3 | 100 | 35.67 | 54.66 | 2 | 0.79 | 10.96 |
| 100×100 | 98.99 | 35.29 | 45.4 | 99.99 | 35.66 | 50.9 | 1 | 0.37 | 5.5 |
| 200×200 | 99.49 | 35.6 | 44.75 | 99.99 | 35.8 | 48 | 0.5 | 0.2 | 3.25 |
Based on the results obtained from Table 3 for the standard GGH algorithm, changing one pixel does not have a deep effect on the cipher image. Therefore, the method requires further improvement which can affect all of the pixels.
According to results in Table 3, the applied padding can affect all the pixels and by changing only one pixel, all of the pixels in the encrypted image will be changed. Also, the Avalanche effect can show the affected bits in the encryption process are performed correctly. The complexity of the applied padding is O(n2) and the complexity of GGH encryption is O(n2), so the whole complexity of the proposed method is O(2n2). By adding a simple padding, the GGH image encryption will be dramatically improved and the cipher becomes resistant to both cipher text and statistical attacks.
From the results, it can be deduced that the performance measurements based on the three measurement criteria including (i) Number of Pixels Change Rate (NPCR), (ii) Unified Average Changing Intensity (UACI), and (iii) Avalanche effect are calculated. The results on three different sizes of images showed that padding based GGH algorithm has improved UACI, NPCR, and Avalanche metrics by almost 100%, 35%, and 45%, respectively, in comparison to the standard GGH algorithm.
In conclusion, this shows that the new proposed method (i.e., padding based GGH algorithm) can be regarded as an improvement to the its fundamental version (i.e., standard GGH algorithm) which acts poorly on all of the UACI, NPCR, and Avalanche metrics.
Moreover, Table 4 has summarized the advantages and disadvantages of various methods discussed in the literature review section and hence, it can also be deduced that all of the encryption methods has their own advantages and shortcomings which need further evaluation to be used in the related position such as medical image encryption. Furthermore, any encryption methodology which has an entropy higher than or almost near to 50% in terms of three measurement criteria can be considered for encrypting the sensitive data.
| Method | Advantages | Disadvantages |
|---|---|---|
| Modified AES Based Algorithm 2007 |
Better performance | Time taking and risky |
| Block-Based Transformation Algorithm, 2008 |
No key generator, correlation between image elements decreased and higher entropy |
Image loosing and lower Correlation |
| Self-Invertible Key Matrix Of Hill Cipher Algorithm, 2008 |
Matrix Based and Encrypt Gray Scale |
Cannot encrypt image with same gray level or color |
| A Combination Of Permutation Technique Followed By Encryption, 2008 |
Higher Entropy and Correlation between image elements decreased |
Permutation process is too complex, Time taking and also chances of mistakes are high |
| A Novel Image Encryption Algorithm Based On Hash Function, 2010 |
Because of encryption done in two phases chances of mistakes is low |
Encryption done in two phases so will be increases |
| A Digital Image Encryption Algorithm Based Composition Of Two Chaotic Logistic Maps, 2010 |
Better than all above because of two logistics maps, Uses external sacred keys and Strong security |
Lot of confusion in process |
| New Modified Version Of Advance Encryption Standard Based Algorithm For Image Encryption, 2010 |
Higher security | The algorithm and the secret key, consequently a same data will be ciphered to the same value; which is the main security weakness. |
| Image Encryption Using Affine Transform And XOR Operation, 2011 |
Better Solution and Correlation between pixels values significantly decreases |
Lengthy, complicated and chances of mistakes is high |
| Permutation Based Image Encryption Technique, 2011 |
Three phases process | High chances of error in key Generation |
| Image Encryption Using Chaotic Maps And DNA Addition Operation And Noise Effects On It, 2011 |
Easy to represent | Not a cost effective process |
| Image Encryption Based On The General Approach For Multiple Chaotic System, 2011 |
Large key space and high-level security, high obscure level and high speed |
Demonstrate process |
| Statistical Analysis Of S-Box In Image Encryption Application Based On Majority Logic Criterion, 2011 |
Correlation analysis, entropy analysis, contrast analysis, homogeneity analysis, energy analysis and mean of absolute deviation analysis |
Complicated and lengthy process because there are lot of analysis done in single technique. Also here time factor will be increases. |
| The Integration Of A Shifting Technique And The AES Algorithm March 2012 |
Improved and effective method | Possibility of mistakes while preparing shifting table, it is lengthy and difficult process |
| Design And Analysis Of A Novel Digital Image Encryption Scheme March 2012 |
Simple, fast and secured against any attack |
Large, complicated and very difficult performance and security analysis |
| Secret Key Encryption Algorithm Using Genetic Algorithm April 2012 |
Encryption method satisfies the goal of encrypting the images |
Complicated and algorithm is too lengthy |
| New Advance Image Encryption To Enhance Security Of Multimedia Concept July 2012 |
Best performance, the lowest correlation and the highest entropy |
Three phase process and every image is very complicated |
| Standard GGH | A good matrix implementation, Lattice based, easy representation, Correct decryption even with less errors, suitable for high resolution pictures | Low entropy, High correlation, needs more bits after encryption |
| Padding based GGH | Same as GGH, Lowest correlation, Highest Entropy | Need more bits for cipher image |
In this study, the avalanche effect of both padding based and standard GGH algorithm has been considered as an important metric for evaluating the cryptography algorithm to illustrate the rate of bit changes in cipher image while only 1 bit change is applied to the original image as defined by Stallings [39]. Based on his studies, if a cryptographic algorithm does not have an avalanche effect value of satisfactory rate, it inherits a poor randomness property which results in good input predictions while only the output is available. Continuously, it has been reported in the literature that if the abovementioned metric value is more than 50% of cipher text bits changed, then the proposed algorithm has a strong avalanche effect [40-43]. The results showed that the avalanche effect value of standard GGH algorithm is almost 10% which is far from the literature standards. However, in some studies the avalanche effect rate values for some well-known cryptography algorithms such as bluefish [44], DES [42], GMDES [42], JEA [41], MUEA [41], AES using binary codes [45], and DES and AES [46] for different applications are reported to be 50%, 50%, 55%,15%, 40%, around 50%-70%, and 43% and 83%, respectively. Based on the results of recent studies and considering the initial avalanche effect of the standard GGH algorithm, it can be easily deduced that the new proposed methodology, the padding based GGH algorithm, has improved the avalanche of the old version by about 45% and has reached the standard avalanche effect values (i.e., more than 50%avalanche effect) of most well-known cryptography algorithms by only adding a padding step before the standard GGH encryption is applied.
Furthermore, according to Table 2, both the standard and the padding based GGH algorithms require n2log2(k) and n2log2(n) bits for private and public keys (R and B), respectively. This means that we don't need any extra memory space for data storage. Regarding the complexities of standard and padding based GGH approaches in terms of key generation, encryption, and decryption, although they have the same complexity of O(n3) considering the key generation process, however, the encryption and decryption complexities of the latter algorithm (i.e., O(2n2)) is twice bigger than those of the former one (i.e., O(n2)). For future researches, improvements [47] can be carried out on different cryptography algorithms such those applied on transposition cipher [48, 49], and Vigener algorithm [50] or taking the advantage of genetic algorithms in generating cipher keys [14] applicable for medical images [13].
CONCLUSION
GGH is a simple public key crypto system which is based on the closest vector problem (CVP). It encrypts data in the matrix form and makes it suitable for image encryption. It works in different dimensions and different square matrices. Experimental studies indicated that changing one pixel in GGH encryption does not have enough effect on the whole encryption output, so a new method is proposed which can add padding to the plain image before applying GGH encryption process. This padding applies the forward and backward snail tour XORing to the plain image in order to make it ready for further process using the GGH encryption algorithm. According to the final results which correspond to the proposed method, changing one pixel affects the whole plain image and also affects the final cipher image reasonably good which is encrypted by GGH algorithm. That is, by changing one pixel, 99.99% of pixels of the cipher image will be changed and also it has a good avalanche effect about 55% which has improved the standard version by more than 45% which shows an acceptable improvement in the whole image encryption to be prune to possible attacks. Moreover, the unified average changing has also dramatically increased and as a result, the GGH snail encryption algorithm is robust and efficient for encrypting medical images in medical image security realm. However, this is a successful study in improving the standard GGH algorithm evaluation metrics especially in terms of avalanche effect, the complexities of encryption and decryption process have been double while compared to the standard version while other parameter remained constant. On the other hand, it is worth considering that the increased complexities can be ignored in comparison to the achieved success (i.e., reach avalanche effect of more than 50%)
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.





