RESEARCH ARTICLE
Do Hummingbirds See in Ultraviolet?
M Curé*, 1, A.G Palacios2
Article Information
Identifiers and Pagination:
Year: 2009Volume: 3
First Page: 9
Last Page: 12
Publisher Id: TOMINFOJ-3-9
DOI: 10.2174/1874431100903010009
Article History:
Received Date: 10/12/2008Revision Received Date: 20/1/2009
Acceptance Date: 15/2/2009
Electronic publication date: 02/4/2009
Collection year: 2009
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
Abstract
We present a numerical model to fit the electroretinogram (ERG), a gross evoked eye visual potential, that originate in the retina through photons absorption by photoreceptors and then involve the contribution form others retinal neurons. We use the ERG measured in a hummingbird, to evaluate the most likely retinal mechanism - cones visual pigments and oil-droplets - that participate in their high dimensional tetra or pentachromatic color hyperspace. The model - a nonlinear fit - appears to be a very useful tool to predict the underlying contribution visual mechanism for a variety of retinal preparation.
1. INTRODUCTION
A critical question in visual sciences is to determinate the types of photoreceptors that contribute - for a particular eye - to the overall retinal spectral sensitivity. We have developed a mathematical model that helps to answer this question. As a case study, we have used the electroretinogram results of a diurnal bird, the firecrown hummingbirds. It has been well established that hummingbirds learn to associate the rich nectar contents of flowers with different colors, varying from red to ultraviolet [1-6] and it is of particular interest to know the neural bases for such chromatic properties. Avian retinae show a complex array of photoreceptors, including single and double cones with visual pigments of maximal absorption sensitivity ( λmax ) at long-wavelength-sensitive cone visual pigment (l-cone) with λmax between 540 nm and 570 nm ; medium-wavelength-sensitive cone visual pigment (M-cone) with λmax between 500 nm and 507 nm ; short-wavelength-sensitive cone visual pigment (S-cone) with λmax between 430 nm and 460nm and violet-wavelength-sensitive cone (V-cone) with λmax (between 400 nm and 420nm ) or ultraviolet-sensitive-cone (UV-cone) with λmax (between 360 nm and 370nm ) [7-9]. A special trait of bird’s cones is the presence of oil-droplets spherical lipid structures inserted in the inner segment of the photoreceptor - which form long pass filters with optical properties that depend on carotenoid contents and concentrations [8] (also see section 2.1.2 below). The V-cone or UV-cone contain a transparent (t) oil-droplet with no carotenoid; the s-cones a galloxanthin (pale appearance); the m-cones a zeaxanthin (yellow appearance); and l-cones an astaxanthin (red) in high concentrations. Double cones have L visual pigments and are screened by a variety of galloxanthin and ε -carotene mixtures [2, 8, 10-12]. The final cone mechanism sensitivity is then determined by combining the cone visual pigment absorption and oil-droplet transmittance. In many birds, ultraviolet (UV) is a color that is believed to be involved in social communication, food or sexual selection and it is of particular interest to know their presence in many vertebrates’ species [13]. We developed a theoretical non-linear model that takes into account the additive - the assumed mode here - combination of the spectral properties of different cones visual pigments and their oil-droplets complements. Here we compare the predictions of this model with the electroretinogram (ERG), a gross retina visual evoke potential, response outcome.
2. THE ELECTRORETINOGRAM (ERG)
All the details of the experimental work are described in detail in [14, 15]. In brief, the optical system consisted of a stabilized power supply with a quartz lamp (250W, ORIEL), a monochromator (1200 lines mm-1 grating, ORIEL, 20 nm half-bandwidth). A short-pass filter (UG11) to isolate the UV band and long-pass filters (SCHOTT RG500 , RG540 , RG680 ) to eliminate stray light from the monochromator, were used. An electronic shutter (Uniblitz, Vincent Associates) was utilized to control flash duration and an optical quartz wedge ( 0 – 5 Optical Density) was inserted to attenuate the flash intensity. The monochromator, optical wedge and shutter were under computer control and adjusted to deliver short flashes at wavelengths from 300 to 700 nm in 20 nm steps. The eye was kept light adapted by a quartz tungsten lamp ( 150W ) producing a background illumination of 240 µW / cm2sr at the cornea. The light stimulus was collimated at the cornea using a quartz condenser. After general anesthesia the ERG signal was recorded using a pair of ring Ag / AgCl electrodes, one placed on the cornea and the other - reference electrode - under the head skin, and amplified with a high gain amplifier (DP-301 Warner Instruments). The ERG spectral sensitivity function S(λ) was calculated from rpeak / I ; where I is the flash photon flux, and rpeak is the b-band peak of the ERG response, evoked by a series of dim flashes ( n = 50 - 100 ). Fig. (1) illustrates a theoretical ERG response, where the a-band responses correspond to the photoreceptors input and the b-band is related to a class of retinal ON bipolar cells.
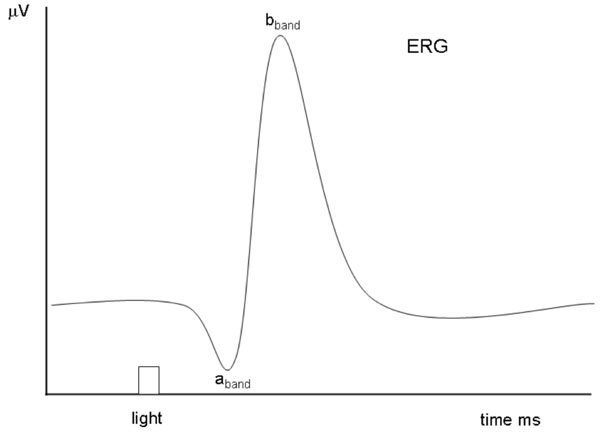 |
Fig. (1). Simulated ERG example showing the different characteristic a-band and b-band evoked by a flash light stimulation. |
2.1. The Pigment’s Functions
2.1.1. The Primary Pigment Function
The photochemistry of visual pigments in the 300 - 700 nm spectral range shows two principal absorption αband and βband peaks. The spectral sensitivity of αband depends on the absorption properties of a chromophore (11-cis retinal) covalently linked to an opsin protein, and follows [16], namely:
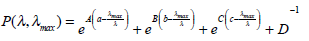 |
(1) |
where a is the visual pigment dependence as function of the wavelength:
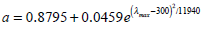 |
(2) |
and λmax refers to the peak absorption. The others constants are: A = 69.7 , B = 28. , C = –14.9 , D = 0.674 , b = 0.922 , c = 1.104. The βband absorption can be estimated using a log-normal function [17] and βλmax location is related to αλmax [18] by:
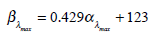 |
(3) |
Finally, the visual pigments are given by:
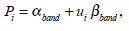 |
(4) |
where ui represent the relative amplitude of the βband. As an example, we show in Fig. (2) the absorption properties of a visual pigment with λmax = 510 nm and ui = 0.26
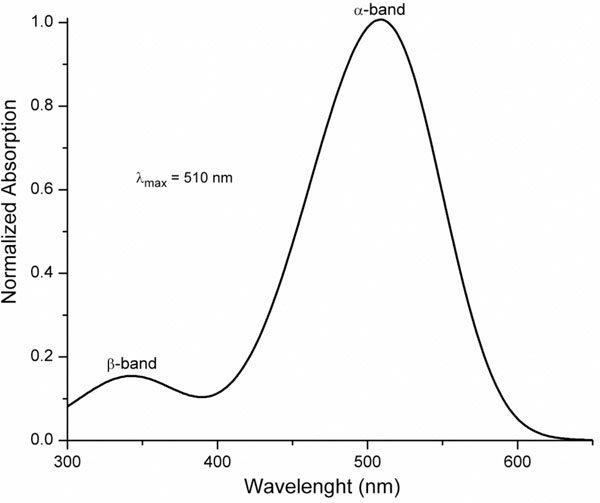 |
Fig. (2). Visual pigment template with λmax = 510 nm and ui = 0.26, calculated using Eqs. 1 to 4. |
3. THE VISUAL PIGMENTS AND THE NON-LINEAR MODEL
According to the above, the spectral response of the ERG can be reproduced by:
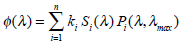 |
(6) |
where n = 5 is the number of different cones in avian retina, i is corresponding index, ki the relative contribution of different chromatic mechanisms, Pi is the absorbance spectra of cones (Eq. 4) and Si is the associated oil-droplets (Eq. 5).
3.1. Parameters Constraints
Before performing fits, we constrain our model by defining ranges of values for certain parameters. The used restrictions are:
- ki ≥ 0 , this is valid for all ki because the contribution to the total sensitivity must be positive.
- 0 ≤c'i≤ 20, this restriction is related to each of oil-droplets pigment concentration associated to each photoreceptor.
- 0.1 ≤ui≤ 0.6 for the βband amplitude due to observed values in the literature [18].
- –5 ≤ λi≤ 5 is valid for all λmax of the αband of different types of cones pigments.
4. THE NON-LINEAR FIT
We want to minimize the following least-square function:
 |
(7) |
where y represents the measured values of the ERG spectral sensitivity and N gives the number of measured data points.
The algorithm we used to find a minimum of this function is the Nelder & Mead downhill simplex algorithm [20]. In order to find the global minimum and not just a local minimum, we run the program many times ( n = 500 ) starting each time with a different set of randomly selected values for the initial parameters.
This procedure give us the global minimum (Ψmin = 0.06347 ) and we proceed to compare the measured data y with the fitted data ø obtained using the parameters of the global minimum. Fig. (3) shows y versus ø, the continuous straight-line shows the linear relationship between them. In view of this linear relationship, we calculated the Pearson correlation index for each one of the runs that we performed. Fig. (4) shows all the minimae founded in our runs plotted against their correlation index.
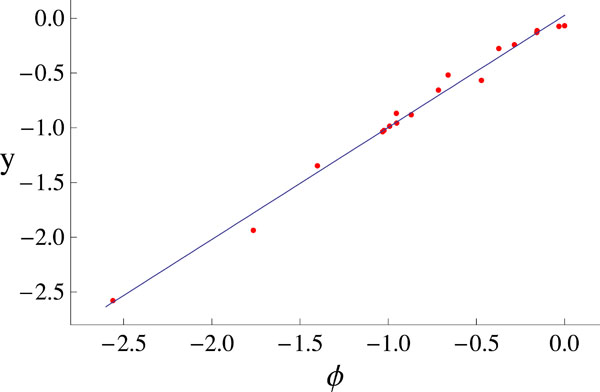 |
Fig. (3). The measured data y versus the fitted data ø. There clearly exhibit a linear relationship. |
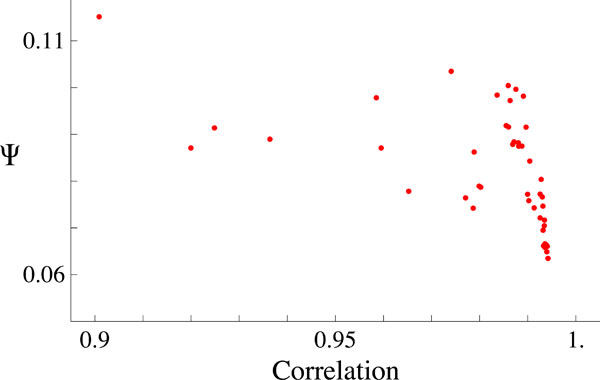 |
Fig. (4). This plot shows all the minima values of Ψ versus the corresponding Pearson’s correlation. The Global minimum is the one with the best correlation. |
The last plot shows clearly that the best fit corresponds to the best Pearson’s correlation, the value of this one is R = 0.9942 . Fig. (5) shows the measured ERG data along with the best fit obtained ø (solid black line) and the relative contribution of each of the visual mechanisms involved (see Eq. 6). Table 1 shows the numerical data illustrated in Fig. (5) and reflects the best fit model.
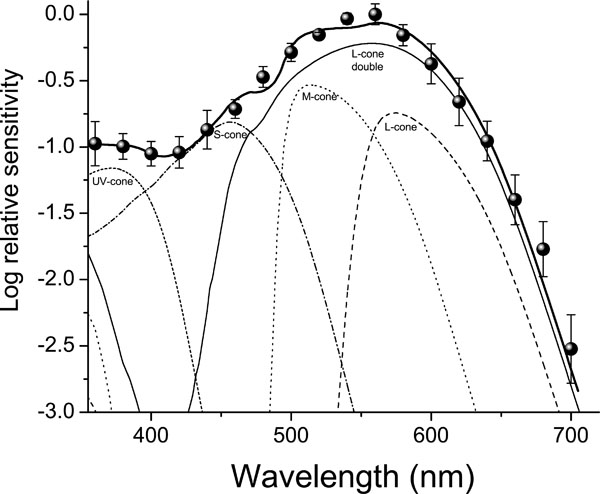 |
Fig. (5). The contribution of each visual mechanism, the total spectral sensitivity and the measured data (see text for details and Table 1 for relative values). |
| Visual Pigment | λ max (nm) | Carotenoid (Optical Density) | Relative Contribution |
|---|---|---|---|
|
|
|||
| L double cone | 560 | 2.0 | 45% |
| L single cone | 560 | 8.0 | 15% |
| M cone | 508 | 3.0 (CisC) | 22% |
| 5.0 (TransC) | |||
| S cone | 444 | 0.3 | 13% |
| UV cone | 371 | - | 5% |
5. CONCLUSION
We model the photopic ERG sensitivity of an avian retina as a function of four singles cones and one double cone mechanism (visual pigment + oil-droplets). In order to get a global minimum we run the simulation process 500 times starting each time with a different random seed. The global minimum that we find corresponds to the highest Pearson correlation coefficient between the ERG data and the best fit obtained. From the best fit we find λmax at 371 nm for the UV-cone; 444 nm for the S-cone; 508 nm for the M-cone and 560 nm for the L-cone (see also Table 1). This result suggests the contribution of five different cone pigments, including one into the UV. One point of precaution is that a definitive proof of the presence of those particular cones mechanism should be confirmed by complementary studies (e.g. Microspectrophotometry, behavioral data; cloning of visual protein genes and its expression absorbance measures in vitro). In general, it has been described that double cones dominate in avian retina (close to 50% of the all types of cones) and their contribution to the ERG is essential and can mask the contribution of other cone mechanisms. While our results confirm double cone contributions they also suggest the participation of four single cone mechanisms. To the best of our knowledge, this is the first work using a numerical model to analyze the ERG, a relative general measure of the eye visual function, by combining contributions of individual cone mechanisms. In recent experiments, we have extended our model application to a trichromatic color vision insect with very promising predictions [21].
An important limitation of the present version of the model is the assumption that the retinal signal of individual mechanism can simply be integrated according to additives rules. As an important neural property, for example, the presence of opponent (subtractive) mechanisms shows vertebrates retina to be involved [22]. Furthermore, we must look to the diversity array of cones in function of behavioral experiments to further explore models to explain color vision in birds [23, 24].
ACKNOWLEDGEMENTS
We thank Servicio Agricola Ganadero (SAG) permission # 1392 for animal captures. Animal care and experimental procedures complied with international regulations (NIH publications Number 80-23). Funding by Fondecyt #1000396 (AGP) and PBCT-CONICYT ACT45 to AGP. Finally, we want to thank M.R. Schreiber for his valuable comments and language help in improving this manuscript.




